温馨提示:本篇内容较长,建议收藏后再看。
一、题目
来百度APP畅享高清图片
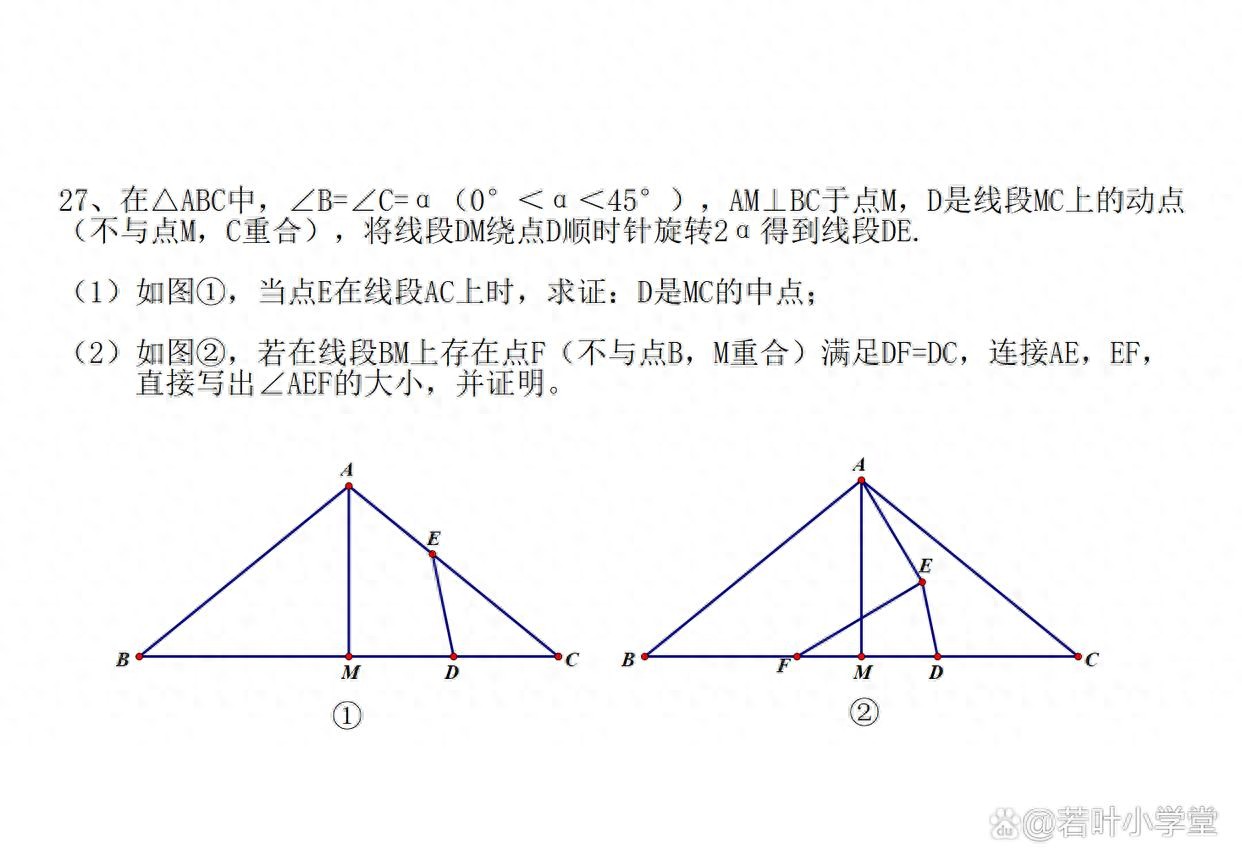
在ABC中,∠B=∠C=α(0°<α<45°),AM⊥BC于点M,D是线段MC上的动点(不与点M,C重合),将线段DM绕点D顺时针旋转2α得到线段DE.
(1)如图①,当点E在线段AC上时,求证:D是MC的中点;
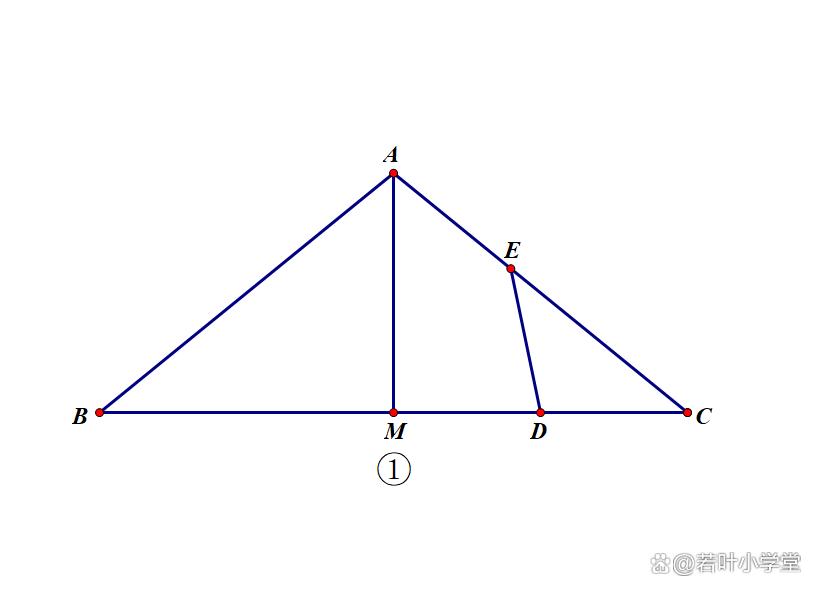
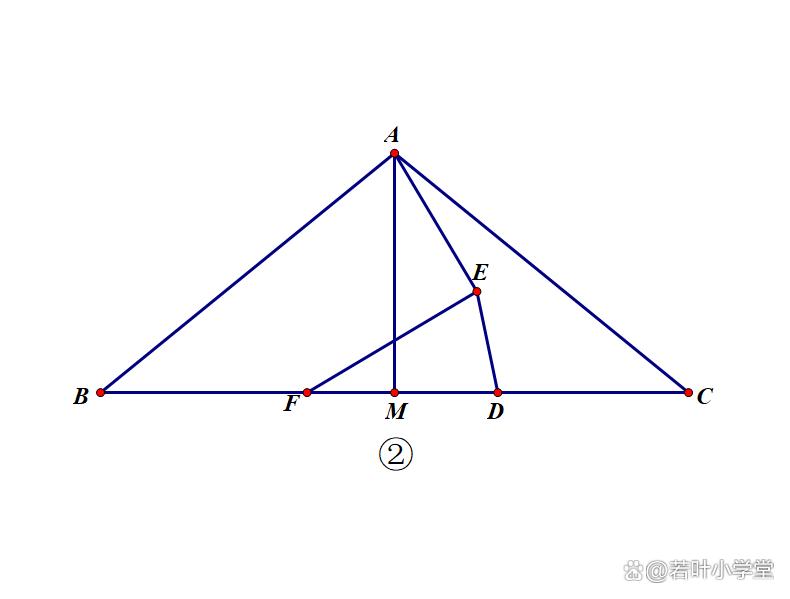
(2)如图②,若在线段BM上存在点F(不与点B,M重合)满足DF=DC,连接AE,EF,直接写出∠AEF的大小,并证明。
二、分析
(1)小题很简单,由2倍角和三角形外角的性质得到等角,然后等角对等边,最后等量代换即证。
(2)小题就比较复杂了。
①猜测结论。
可以直接盲猜90°,也可以简单分析:题目中没告知角度,却要求角度,这类题一般都是特殊角度,再结合图形观察,确定为90°.
②挖掘整理已知条件
a.两中点:M是BC中点,D是FC中点。
可想到双中点模型初中数学:双角平分线模型与双中点模型,特殊三角形(直角三角形或等腰三角形)的中线,中位线,倍长中线。
b.两等边:AB=AC,DM=DE.
可想到等腰三角形,全等三角形。
c.二倍角:∠MDE=2∠C=2∠B
可想到角平分线,等腰三角形顶角的外角,圆心角和圆周角。
d.一垂直:AM⊥BC.
可想到垂直平分线,等腰三角形的三线合一,直角三角形斜边上的中线等于斜边的一半,直径对直角。
e.一平分:AM平分∠BAC.
可想到角平分线的性质和判定,等腰三角形的三线合一,2倍角
f.旋转构图。
旋转出等腰,旋转全等(手拉手全等模型),旋转相似(手拉手相似模型或一转成双)
③从问题入手
如何证垂直?
a.等腰三角形的三线合一
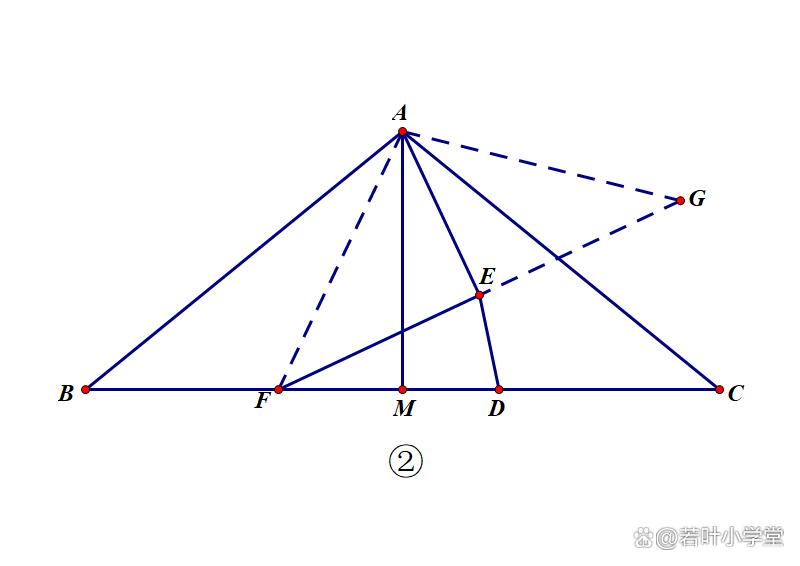
延长FE到点G,使EG=EF,转化为证AF=AG
继续连接CG,转化为证ABF≌ACG,同时DE成为FCG的中位线
b.全等于已知的直角三角形
c.相似于已知的直角三角形

连接AF,证ABM∽AFE
由旋转相似知,连接EM后,可转化为证ABF∽AME手拉手模型拓展:旋转相似,一转成双
d.直径对直角
证点E在以AF为直径的圆上(四点共圆)初中几何:四点共圆的九种判定方法
e.一边上的中线等于这边的一半
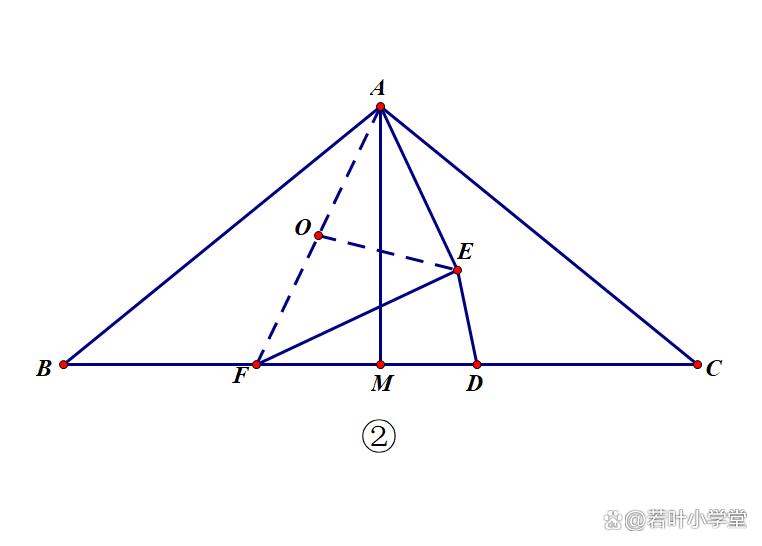
证OE=OA=OF,可利用等腰三角形的性质和三角形内角和进一步得到∠AEF=90°,或直接利用四点共圆得到∠AEF=90°
f.8字模型(角度模型)
证∠EAM=∠EFM
三、解答
(1)证明:由旋转,知 DM=DE,∠MDE=2α
∵∠MDE=∠C+∠DEC=α+∠DEC=2α
∴∠DEC=α=∠C
∴DE=DC ∴DM=DC
即D是MC的中点。
(2)五种方法
解:∠AEF=90°
简证1:对应思路a,由等腰三角形三线合一证垂直,构造手拉手全等图。
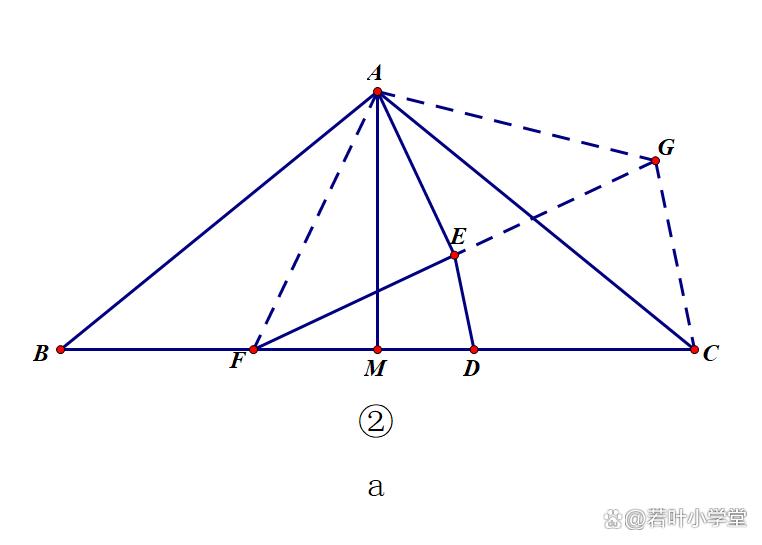
延长FE至点G,使EG=EF,连接AF,AG,CG.
由中位线定理,得 CG//DE,DE=1/2CG,
∴∠MDE=∠ACM+∠ACG
∴∠ACG=∠MDE-∠ACM=2α-α=α=∠B
由双中点模型,得 DM=1/2BF
又∵DE=1/2CG,DM=DE
∴BF=CG 又∵AB=AC
∴ABF≌ACG
∴AF=AG 又∵EF=EG
∴AE⊥EF ∴∠AEF=90°
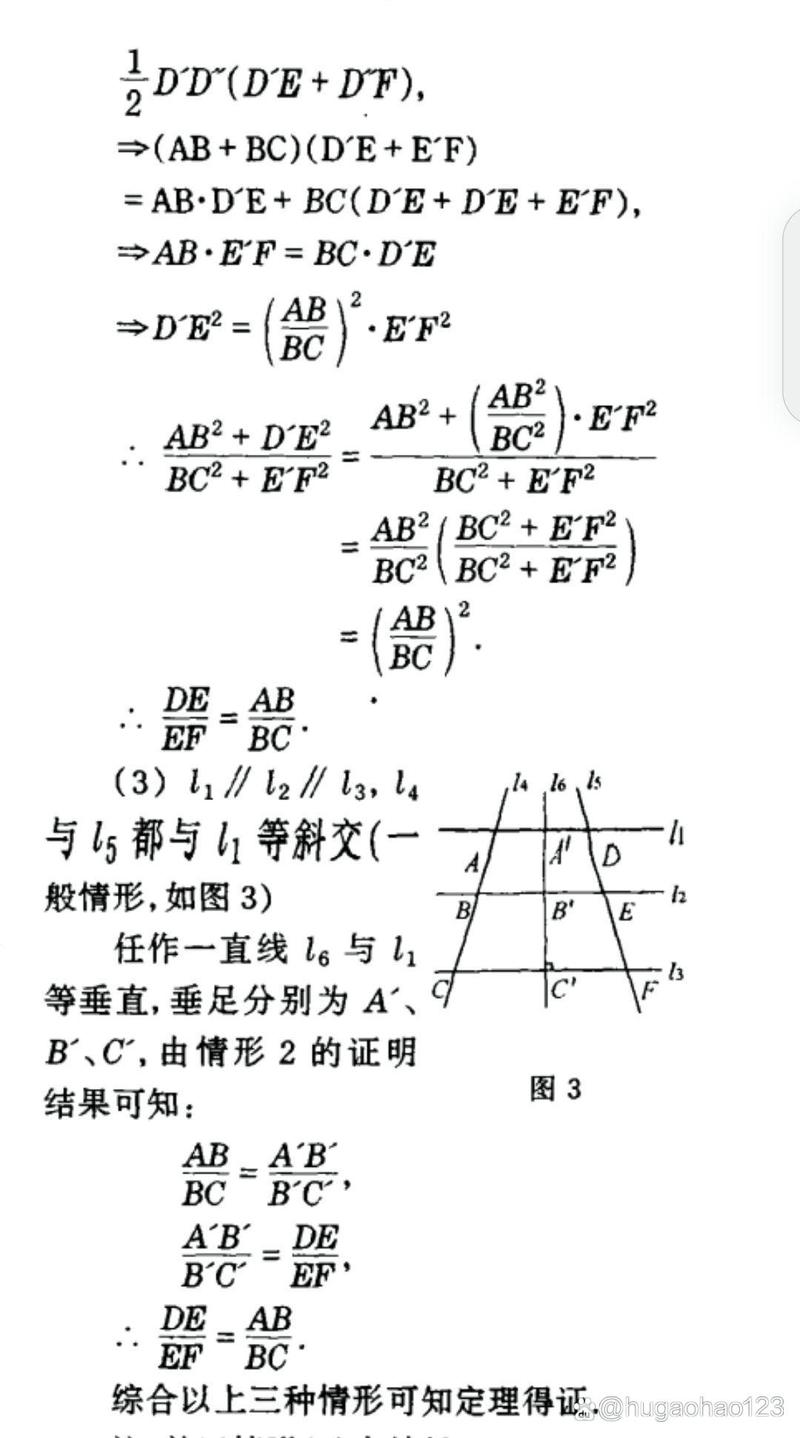
简证2:对应思路c,构造旋转相似。
连接AF,EM,过点D作DG⊥EM于点G
则∠MDG=1/2∠MDE=α,GM=1/2EM
∠AME=α(同角的余角相等)
sin∠ABM=sinα=AM/AB
sin∠MDG=sinα=GM/MD=1/2EM/(1/2BF)=EM/BF
∴AM/AB=EM/BF
∴ABF∽AME
∴ABM∽AFE(旋转相似模型)
∴∠AMB=∠AEF=90°
简证3:对应思路d,主要运用四点共圆和直径对直角。
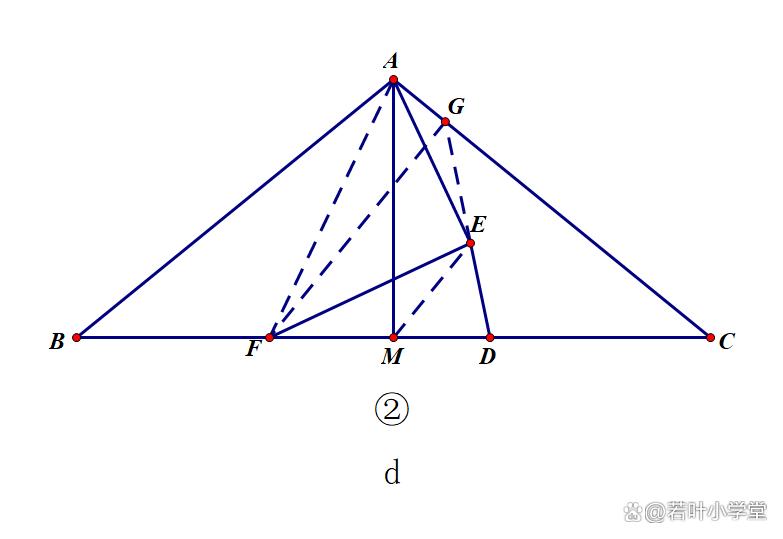
延长DE交AC于点G,连接GF,AF,EM
由(1)结论知,DF=DG=DC
∴点G在以CF为直径的圆上(距点相等,点共圆)
∴∠CGF=90°
∴∠AGF=∠AMF=90°
∴A,F,M,G四点共圆(共边同侧对角等,四点共圆)
∵∠DME=∠DGF
∴F,M,E,G四点共圆(外角等于内对角,四点共圆)
∴A,F,M,E,G五点共圆
∴∠AEF=∠AMF=90°
简证4:对应思路e,利用一边上的中线等于这边的一半来证直角。
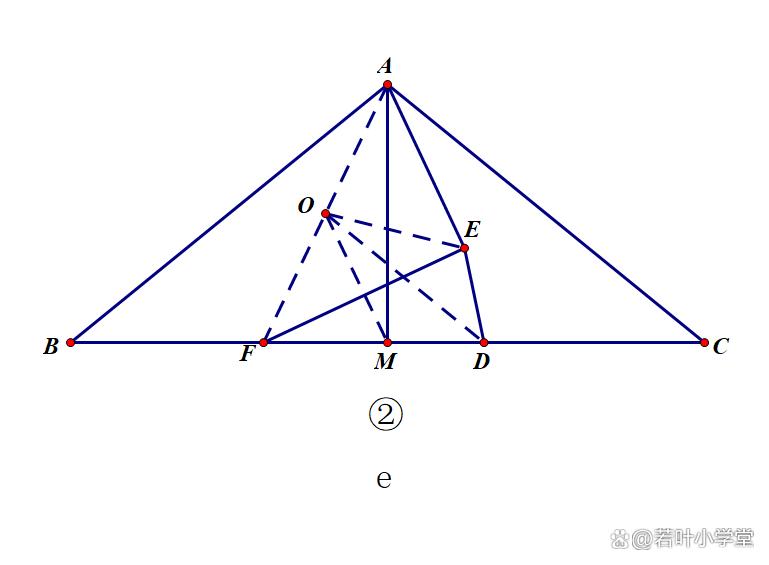
连接AF,取AF中点O,连接OE,OD,OM
∵∠AMF=90°
∴OM=OA=OF
∵OD是FAC的中位线
∴∠ODM=∠C=α=∠ODE
又∵DM=DE,OD=OD
∴ODM≌ODE
∴OM=OE
∴OE=OA=OF
∴∠AEF=90°
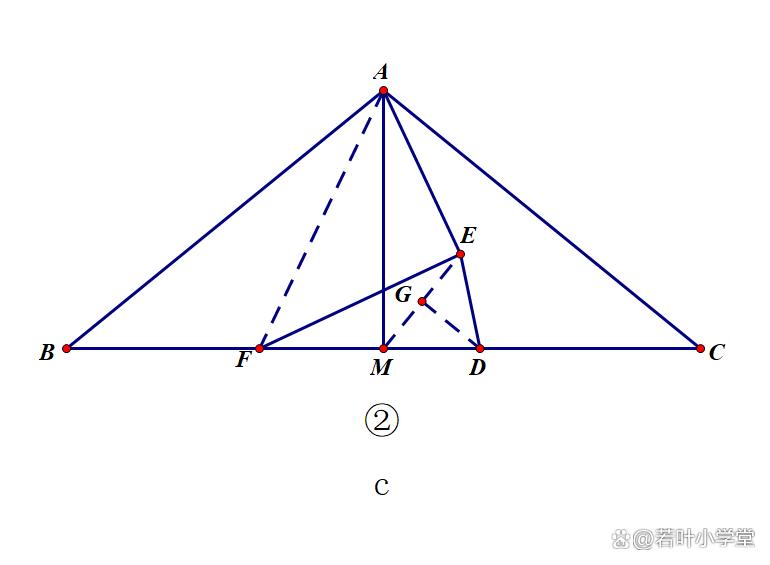
简证5:对应思路f,倍长类中线,8字全等角相等+旋转相似,最终得到8字等角。
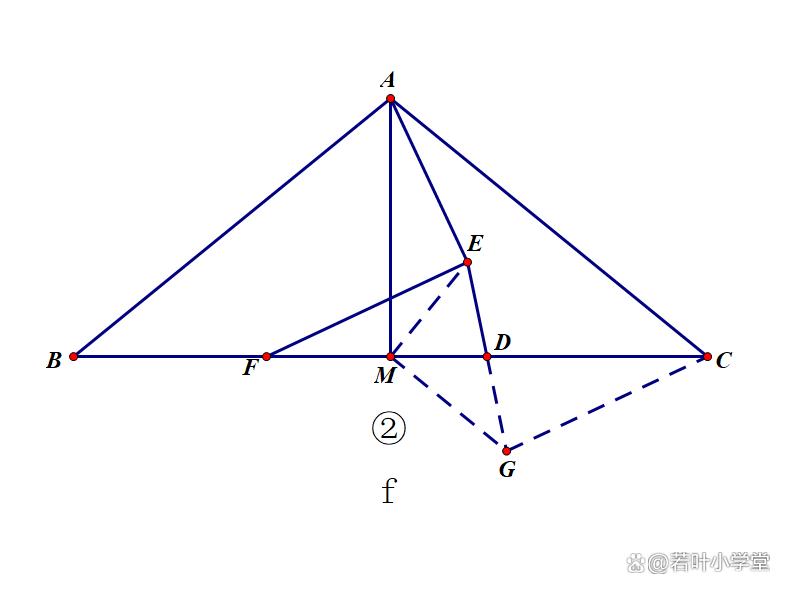
延长ED至点G,使DG=DE,连接EM,GM,GC
易证DEF≌DGC ∴∠DFE=∠DCG
∵DM=DE=DG ∴∠EMG=90°
∴∠AME=∠CMG
∵∠EDM=2α,DE=DM
∴∠DEM=90°-α ∴∠EGM=α
∴tanα=AM/MC=EM/MG
∴AME∽CMG
∴∠EAM=∠GCM
∴∠EAM=∠EFM
由8字模型可得
∠AEF=∠AMF=90°
